Diversity in Competitive Threshold Linear Networks
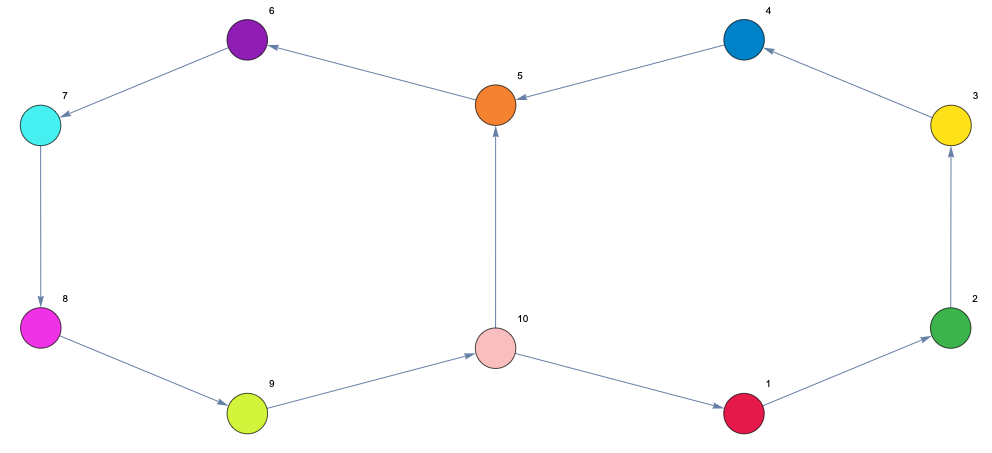 Figure 1 — Directed Network Which Represents Threshold Linear Network
Figure 1 — Directed Network Which Represents Threshold Linear Network
Adjacency Matrix Representing Directed Network
$$\begin{pmatrix} 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\end{pmatrix}$$
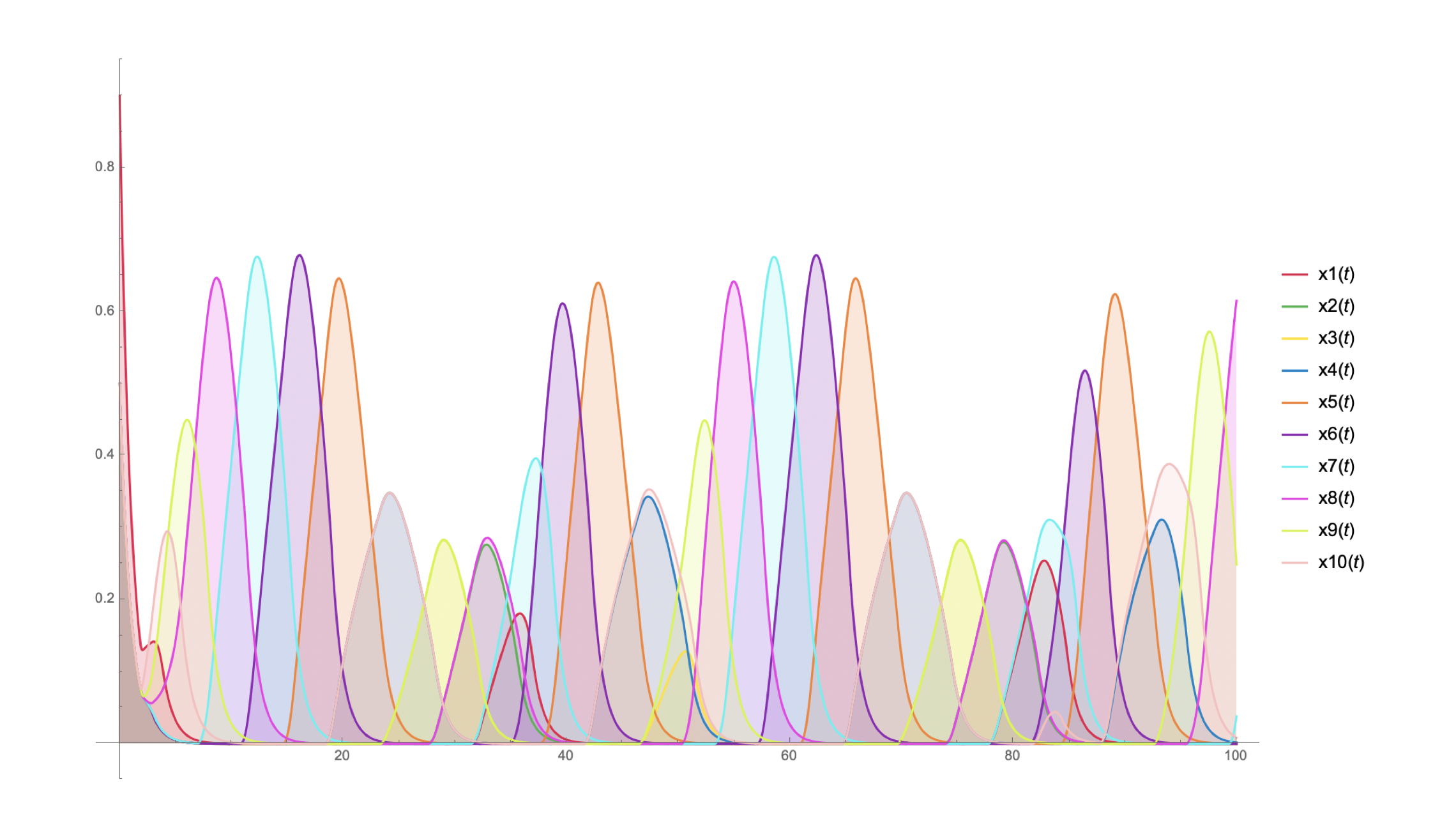 Figure 2 — Solution Via Numerically Solving Differential Equation
Figure 2 — Solution Via Numerically Solving Differential Equation
Initial Conditions
The initial conditions applied to the network above are the following:
- $x1[0] = .9$
- $x2[0] = x3[0] = x4[0] = x5[0] = x6[0] = x7[0] = x8[0] = x9[0] = x10[0] = .5$
 Figure 3 — Dynamics of Directed Network Which Represents Competitive Threshold Linear Network
Figure 3 — Dynamics of Directed Network Which Represents Competitive Threshold Linear Network