K-Means Clustering From Scratch

1 July 2021

Introduction

Imagine we have a scattering of points whose labels or group assignments are completely unknown to us and moreover, we haven’t a clue as to the number of groups. Unsupervised clustering helps us in such a situation and allows us to assign a cluster to each point. These clusters are defined by their centroids (centers). The K-Means algorithm will iteratively update these centroids to find the best location for them. It turns out that this clustering problem that K-Means helps solve is a computationally difficult problem (NP-Hard) but nevertheless we will go through the steps in detail here.

It may help understand this algorithm if we were to create the K-Means algorithm completely from scratch to get a deeper understanding of what is happening. This article includes:

Simulate data
Create functions used by K-Means
Perform K-Means with specified number of clusters
Define a score value, perform K-Means with different number of clusters, and choosing the best value for this hyperparameter
Performing K-Means with the Scikit-Learn library
Compare performance between our implementation and the Scikit-Learn implementation

1. Simulate Data

Let’s begin with simply simulating some points that we will then use to cluster

import random
import numpy as np
import matplotlib.pyplot as plt

n = 100
points = [[random.choice([-1, 1]) + random.uniform(-0.8, 0.8) for _ in range(2)] for _ in range(n)]

[p.append(0) for p in points]
npoints = np.array(points)

plt.scatter(npoints[:,0], npoints[:,1], marker='o', c='r')
plt.title('Scatter Plot of Points')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()

png

2. Define Functions For K-Means

Initialize Clusters

Have k-means algorithm ‘find’ the clusters
Begin by randomly choosing initial cluster values
As we know with k-means, k should be chosen in the beginning. Say we didn’t know there were four clusters in reality so we start with $k = 3$
To choose initial clusters, let’s take a sample of our data, calculate the means of our $X$ and $Y$ values and assign this to a cluster
Let’s say we take a small number of samples just to get rough starting clustering

def initialize_clusters(points, k):

    clusters = [0 for _ in range(k)]

    for i in range(len(clusters)):
        idx = np.random.randint(points.shape[0], size=5)
        sample = points[idx, :]
        clusters[i] = np.mean(sample, axis=0)
        clusters[i][-1] = i

    return np.array(clusters)

k = 3
clusters = initialize_clusters(npoints, k)

Assign Points to a Cluster

Let’s go ahead and assign each point to a cluster depending on which one it is closest to
We will need a distance method to define ‘closeness’
We will also need a method that allows us to compare each point to all clusters and choose the closes

def distance(a, b):
    return np.sqrt((b[0] - a[0])**2 + (b[1] - a[1])**2)

def assign_labels(points, clusters):

    lpoints = np.empty((0, 3))

    for p in points:

        cluster_dist = []
        for c in clusters:
            cluster_dist.append(distance(p, c))

        p[2] = np.argmin(cluster_dist)
        lpoints = np.vstack((lpoints, p))
    
    return lpoints

lpoints = assign_labels(npoints, clusters)

x = lpoints[:, 0]
y = lpoints[:, 1]
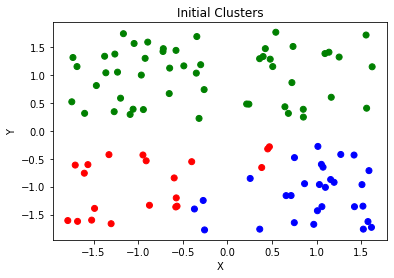
l = lpoints[:, 2]

colors=['r','b','g']
plt.scatter(x, y, c = [colors[int(i)] for i in l])
plt.title('Initial Clusters')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()

png

Update Clusters

Now that we have initial clusters, we can recalculate the clusters

def calculate_clusters(points):
    
    cluster_label = list(set(points[:,2]))
    clusters = []
    
    for c in cluster_label:
        mask = points[:, 2] == c
        clusters.append(np.mean(points[mask, :], axis=0))
        
    return np.array(clusters)

calculate_clusters(npoints)

array([[-0.90555932, -0.95877451,  0.        ],
       [ 0.94987571, -1.12258394,  1.        ],
       [-0.24173413,  1.00161447,  2.        ]])

These are the functions needed to perform K-Means. All we have left to do is iteratively apply these functions to obtain optimal values for our clusters.

3. Perform K-Means with $k = 3$

Generate new data and assign all points to the same group

n = 100
points = [[random.choice([-1, 1]) + random.uniform(-0.8, 0.8) for _ in range(2)] for _ in range(n)]

[p.append(0) for p in points]
npoints = np.array(points)

k = 3
iterations = 30

clusters = initialize_clusters(npoints, k)

for _ in range(iterations):
    # Assign points to clusters
    npoints = assign_labels(npoints, clusters)
    # Update cluster
    clusters = calculate_clusters(npoints)

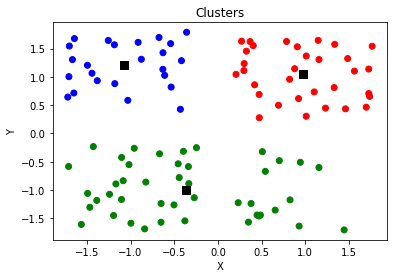
x = npoints[:, 0]
y = npoints[:, 1]
l = npoints[:, 2]

colors=['r','b','g', 'k', 'y']
plt.scatter(x, y, c = [colors[int(i)] for i in l])
plt.scatter(clusters[:,0],clusters[:,1],s=70,marker='s',c='k')
plt.title('Clusters')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()

png

4. Finding Best Value For $k$

We can calculate the sum of squared distances between all points and their respective clusters

def calculate_score(points, clusters):
    
    dist_list = []
    for p in points:
        dist_list.append(distance(p, clusters[int(p[2])])**2)

    return sum(dist_list)

calculate_score(npoints, clusters)

63.98898775077078

Iterate through and find best $k$ value by plotting Elbow

iterations = 50
scores = []
colors=['C' + str(i) for i in range(10)]

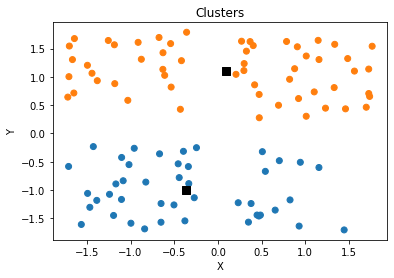
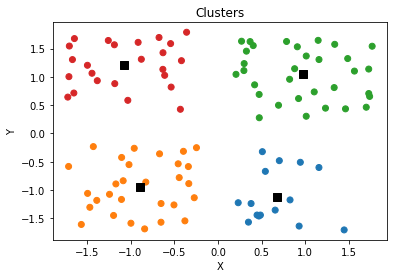
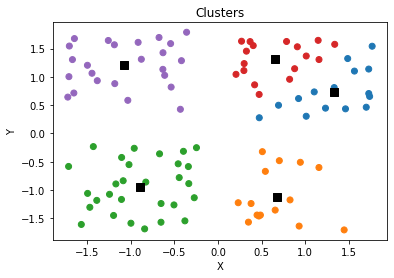
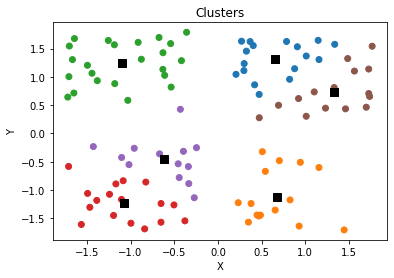
for k in range(1, 10):
    
    clusters = initialize_clusters(npoints, k)

    for _ in range(iterations):
        # Assign points to clusters
        npoints = assign_labels(npoints, clusters)
        # Update cluster
        clusters = calculate_clusters(npoints)
    
    scores.append([k, calculate_score(npoints, clusters)])
    
    x = npoints[:, 0]
    y = npoints[:, 1]
    l = npoints[:, 2]
    plt.scatter(x, y, c = [colors[int(i)] for i in l])
    plt.scatter(clusters[:,0],clusters[:,1],s=70,marker='s',c='k')
    plt.title('Clusters')
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.show()

png

plt.plot([s[0] for s in scores], [s[1] for s in scores], 'ro-')
plt.title('Elbow Plot')
plt.xlabel('k (Number of Clusters)')
plt.ylabel('Sum of Within Sum of Squared Errors')
plt.show()

png

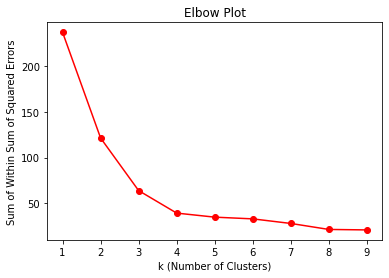
Found Optimal Hyperparameter, $k$

We find that 4 is the optimal number of clusters which was the number of clusters used to simulate the original data (with noise).

5. Using ScikitLearn Library

Although we show how KMeans may be implemented ourselves with a few simple ideas, we can take advantage of libraries as well such as ScikitLearn. In fact, it only takes one line!

from sklearn.cluster import KMeans

y_pred = KMeans(n_clusters=4, random_state=0).fit(npoints[:, :2])

x = npoints[:, 0]
y = npoints[:, 1]
l = y_pred.labels_
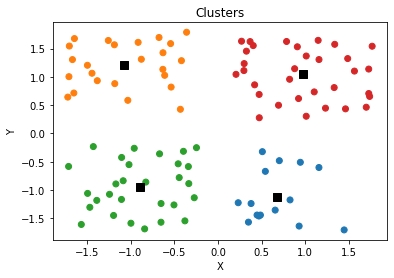
plt.scatter(x, y, c = [colors[int(i)] for i in l])
plt.scatter(y_pred.cluster_centers_[:,0], y_pred.cluster_centers_[:,1],s=70,marker='s',c='k')
plt.title('Clusters')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()

png

y_pred.inertia_

39.46338949369036

6. Comparing Performance

When compared to the scores we obtained from scrach (when $k = 4$), the scores are VERY similar! Just compare the “inertia” above with the score for $k = 4$ below.

scores

[[1, 236.5967940882629],
 [2, 121.32804203454275],
 [3, 63.98898775077078],
 [4, 39.46338949369035],
 [5, 35.048952764699855],
 [6, 33.172015160724094],
 [7, 28.18150296713385],
 [8, 21.647161881862452],
 [9, 21.134201520090667]]

Conclusion

Pros

Relatively simple to implement.
Scales to large data sets.
Guarantees convergence.
Can warm-start the positions of centroids.
Easily adapts to new examples.
Generalizes to clusters of different shapes and sizes, such as elliptical clusters.

Cons

Must choose $k$ manually
Quite dependent on initial centroids
Clustering data of different sizes and densities
Clusters could be ‘dragged’ by outliers (they may even get their own cluster)
Scales poorly with high number of dimensions (consider projecting data points into lower dimensional space using PCA)

We’ve completed all of our tasks and hopefully you have a better idea of how the K-Means algorithm works and how to implement it by hand if you needed to.